regression lineaire python

Régression

L’analyse de régression est l’un des domaines les plus importants des statistiques et de l’apprentissage automatique. Il existe de nombreuses méthodes de régression disponibles. La régression linéaire en fait partie.

Régression linéaire

La régression linéaire est probablement l’une des techniques de régression les plus importantes et les plus utilisées. C’est l’une des méthodes de régression les plus simples. L’un de ses principaux avantages est la facilité d’interprétation des résultats.

Régression linéaire simple

La régression linéaire simple ou à variable unique est le cas le plus simple de régression linéaire, car elle comporte une seule variable indépendante, 𝐱 = 𝑥.

La figure suivante illustre une régression linéaire simple :

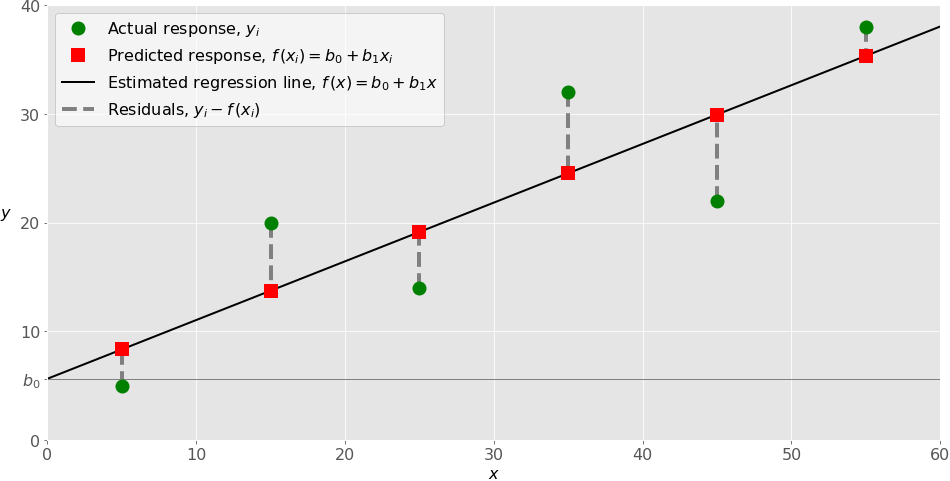
Lors de la mise en œuvre d’une régression linéaire simple, vous commencez généralement avec un ensemble donné de paires entrée-sortie (𝑥-𝑦). Ces paires sont vos observations, représentées par des cercles verts sur la figure. Par exemple, l’observation la plus à gauche a l’entrée 𝑥 = 5 et la sortie réelle, ou réponse, 𝑦 = 5. L’observation suivante a 𝑥 = 15 et 𝑦 = 20, et ainsi de suite.

La fonction de régression estimée, représentée par la ligne noire, a l’équation 𝑓(𝑥) = 𝑏₀ + 𝑏₁𝑥. Votre objectif est de calculer les valeurs optimales des poids prédits 𝑏₀ et 𝑏₁ qui minimisent le SSR et de déterminer la fonction de régression estimée.

La valeur de 𝑏₀, également appelée ordonnée à l’origine , montre le point où la droite de régression estimée coupe l’axe 𝑦. C’est la valeur de la réponse estimée 𝑓(𝑥) pour 𝑥 = 0. La valeur de 𝑏₁ détermine la pente de la droite de régression estimée.

Les réponses prédites, représentées par des carrés rouges, sont les points sur la droite de régression qui correspondent aux valeurs d’entrée. Par exemple, pour l’entrée 𝑥 = 5, la réponse prédite est 𝑓(5) = 8,33, ce que représente le carré rouge le plus à gauche.

Les lignes grises pointillées verticales représentent les résidus, qui peuvent être calculés comme 𝑦ᵢ – 𝑓(𝐱ᵢ) = 𝑦ᵢ – 𝑏₀ – 𝑏₁𝑥ᵢ pour 𝑖 = 1, …, 𝑛. Ce sont les distances entre les cercles verts et les carrés rouges. Lorsque vous implémentez la régression linéaire, vous essayez en fait de minimiser ces distances et de rendre les carrés rouges aussi proches que possible des cercles verts prédéfinis.

Sous-ajustement et surajustement

Une question très importante qui peut se poser lors de la mise en œuvre d’une régression polynomiale est liée au choix du degré optimal de la fonction de régression polynomiale.

Il n’y a pas de règle simple pour ce faire. Cela dépend des cas. Vous devez cependant être conscient de deux problèmes qui peuvent découler du choix du diplôme : le sous-apprentissage et le surapprentissage .

Le sous-ajustement se produit lorsqu’un modèle ne peut pas capturer avec précision les dépendances entre les données, généralement en raison de sa propre simplicité. Cela donne souvent un 𝑅² faible avec des données connues et de mauvaises capacités de généralisation lorsqu’il est appliqué avec de nouvelles données.

Le surajustement se produit lorsqu’un modèle apprend à la fois les dépendances des données et les fluctuations aléatoires. En d’autres termes, un modèle apprend trop bien les données existantes. Les modèles complexes, qui comportent de nombreuses fonctionnalités ou termes, sont souvent sujets au surapprentissage. Lorsqu’ils sont appliqués à des données connues, de tels modèles donnent généralement un 𝑅² élevé. Cependant, ils ne généralisent souvent pas bien et ont un 𝑅² nettement inférieur lorsqu’ils sont utilisés avec de nouvelles données.

La figure suivante illustre les modèles sous-équipés, bien ajustés et suréquipés :

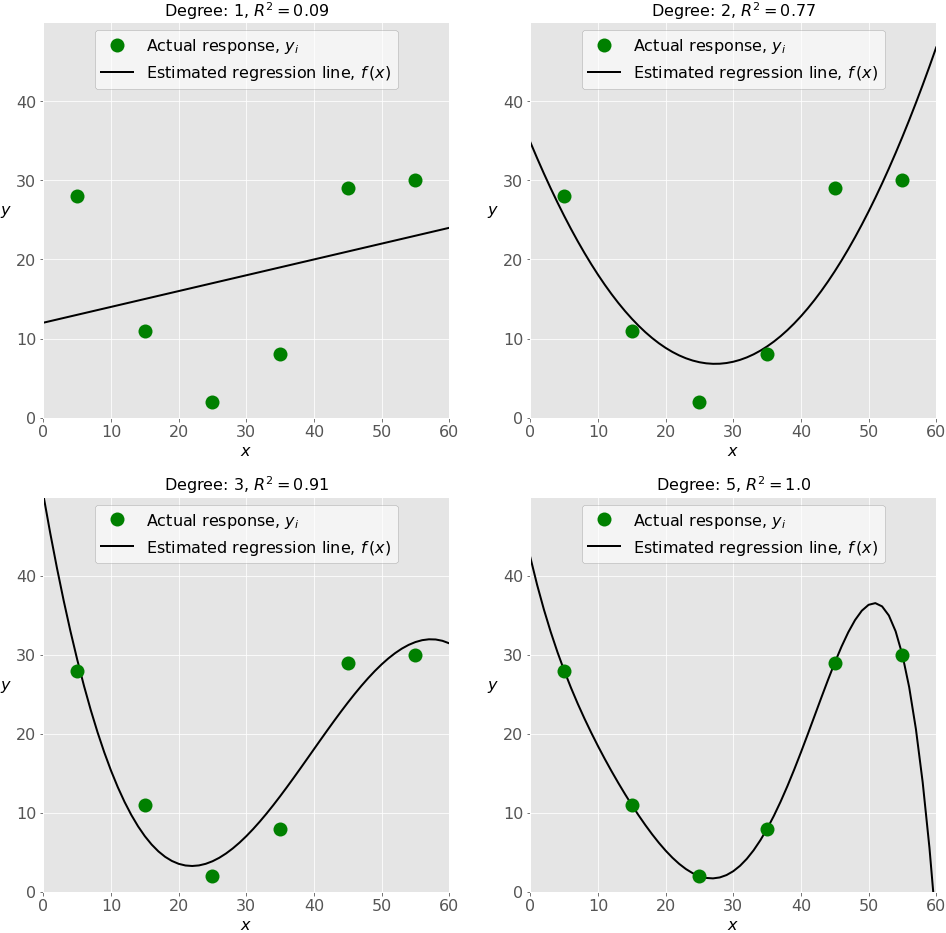
Le graphique en haut à gauche montre une droite de régression linéaire qui a un 𝑅² faible. Il peut également être important qu’une ligne droite ne puisse pas prendre en compte le fait que la réponse réelle augmente à mesure que 𝑥 s’éloigne de vingt-cinq et se rapproche de zéro. Il s’agit probablement d’un exemple de sous-apprentissage.

Le graphique en haut à droite illustre la régression polynomiale avec un degré égal à deux. Dans ce cas, cela pourrait être le degré optimal pour modéliser ces données. Le modèle a une valeur de 𝑅² qui est satisfaisante dans de nombreux cas et montre bien les tendances.

Le graphique en bas à gauche présente une régression polynomiale avec un degré égal à trois. La valeur de 𝑅² est plus élevée que dans les cas précédents. Ce modèle se comporte mieux avec les données connues que les précédents. Cependant, il montre des signes de surajustement, en particulier pour les valeurs d’entrée proches de 6y, où la ligne commence à diminuer, bien que les données réelles ne le montrent pas.

Enfin, sur le graphique en bas à droite, vous pouvez voir l’ajustement parfait : six points et la droite polynomiale de degré cinq (ou plus) donnent 𝑅² = 1. Chaque réponse réelle est égale à sa prédiction correspondante.

Dans certaines situations, cela peut être exactement ce que vous recherchez. Toutefois, dans de nombreux cas, il s’agit d’un modèle suréquipé. Il est probable qu’il ait un mauvais comportement avec des données invisibles, en particulier avec des entrées supérieures à cinquante.

Par exemple, cela suppose, sans aucune preuve, qu’il y a une baisse significative des réponses pour 𝑥 supérieur à cinquante et que 𝑦 atteint zéro pour 𝑥 proche de soixante. Un tel comportement est la conséquence d’un effort excessif pour apprendre et ajuster les données existantes.

Il existe de nombreuses ressources où vous pouvez trouver plus d’informations sur la régression en général et la régression linéaire en particulier. La page d’analyse de régression sur Wikipédia , l’entrée sur la régression linéaire de Wikipédia et l’article sur la régression linéaire de la Khan Academy sont de bons points de départ.

Packages Python pour la régression linéaire

Il est temps de commencer à implémenter la régression linéaire en Python. Pour ce faire, vous appliquerez les packages appropriés ainsi que leurs fonctions et classes.

NumPy est un package scientifique Python fondamental qui permet de nombreuses opérations hautes performances sur des tableaux unidimensionnels et multidimensionnels. Il propose également de nombreuses routines mathématiques. Bien sûr, c’est open source.

Si vous n’êtes pas familier avec NumPy, vous pouvez utiliser le guide de l’utilisateur officiel de NumPy et lire Tutoriel NumPy : Vos premiers pas dans la science des données en Python . De plus, Look Ma, No forLoops: Array Programming With NumPy et Pure Python vs NumPy vs TensorFlow Performance Comparison peut vous donner une bonne idée des gains de performances que vous pouvez obtenir en appliquant NumPy.

Le package scikit-learn est une bibliothèque Python largement utilisée pour l’apprentissage automatique, construite sur NumPy et quelques autres packages. Il fournit les moyens de prétraiter les données, de réduire la dimensionnalité, de mettre en œuvre la régression, la classification, le regroupement, etc. Comme NumPy, scikit-learn est également open source.

Vous pouvez consulter la page Modèles linéaires généralisés sur le site Web scikit-learn pour en savoir plus sur les modèles linéaires et mieux comprendre le fonctionnement de ce package.

Si vous souhaitez implémenter une régression linéaire et avez besoin de fonctionnalités dépassant la portée de scikit-learn, vous devriez envisager statsmodels . Il s’agit d’un package Python puissant pour l’estimation de modèles statistiques, la réalisation de tests, etc. C’est également open source.

Vous pouvez trouver plus d’informations sur les modèles de statistiques sur son site officiel .

Maintenant, pour suivre ce tutoriel, vous devez installer tous ces packages dans un environnement virtuel :

(venv) $ python -m pip install numpy scikit-learn statsmodels

Cela installera NumPy, scikit-learn, statsmodels et leurs dépendances.

Régression linéaire simple avec scikit-learn

Vous commencerez par le cas le plus simple, à savoir la régression linéaire simple. Il y a cinq étapes de base lorsque vous implémentez une régression linéaire :

1. Importez les packages et les classes dont vous avez besoin.
2. Fournissez des données avec lesquelles travailler et effectuez éventuellement les transformations appropriées.
3. Créez un modèle de régression et adaptez-le aux données existantes.
4. Vérifiez les résultats de l’ajustement du modèle pour savoir si le modèle est satisfaisant.
5. Appliquez le modèle pour les prédictions.

Ces étapes sont plus ou moins générales pour la plupart des approches et implémentations de régression. Tout au long du reste du didacticiel, vous apprendrez comment effectuer ces étapes pour plusieurs scénarios différents.

Étape 1 : Importer des packages et des classes

La première étape consiste à importer le package numpyet la classe LinearRegressiondepuis sklearn.linear_model:

>>> import numpy as np
>>> from sklearn.linear_model import LinearRegression

Vous disposez désormais de toutes les fonctionnalités dont vous avez besoin pour implémenter la régression linéaire.

Le type de données fondamental de NumPy est le type de tableau appelé numpy.ndarray. Le reste de ce didacticiel utilise le terme tableau pour désigner les instances du type numpy.ndarray.

Vous utiliserez la classe sklearn.linear_model.LinearRegressionpour effectuer une régression linéaire et polynomiale et faire des prédictions en conséquence.

Étape 2 : Fournissez les données

La deuxième étape consiste à définir les données avec lesquelles travailler. Les entrées (régresseurs, 𝑥) et la sortie (réponse, 𝑦) doivent être des tableaux ou des objets similaires. Il s’agit de la manière la plus simple de fournir des données pour la régression :

>>> x = np.array([5, 15, 25, 35, 45, 55]).reshape((-1, 1))
>>> y = np.array([5, 20, 14, 32, 22, 38])

Vous disposez désormais de deux tableaux : l’entrée, xet la sortie, y. Vous devriez faire appel .reshape()car xce tableau doit être bidimensionnel , ou plus précisément, il doit avoir une colonne et autant de lignes que nécessaire . C’est exactement ce que précise l’argument (-1, 1)de .reshape().

Voici comment xet yregardez maintenant :

>>> x
array([[ 5],
       [15],
       [25],
       [35],
       [45],
       [55]])

>>> y
array([ 5, 20, 14, 32, 22, 38])

Comme vous pouvez le voir, xa deux dimensions et x.shapeest (6, 1), tandis qu’il ya une seule dimension et y.shapeest (6,).

Étape 3 : Créez un modèle et ajustez-le

L’étape suivante consiste à créer un modèle de régression linéaire et à l’ajuster à l’aide des données existantes.

Créez une instance de la classe LinearRegression, qui représentera le modèle de régression :

>>> model = LinearRegression()

Cette instruction crée la variable model en tant qu’instance de LinearRegression. Vous pouvez fournir plusieurs paramètres facultatifs pourLinearRegression :

• fit_interceptest un booléen qui, si True, décide de calculer l’ordonnée à l’origine 𝑏₀ ou, si False, la considère égale à zéro. La valeur par défaut est True.
• normalizeest un booléen qui, si True, décide de normaliser les variables d’entrée. Sa valeur par défaut est False, auquel cas il ne normalise pas les variables d’entrée.
• copy_Xest un booléen qui décide s’il faut copier ( True) ou écraser les variables d’entrée ( False). C’est Truepar défaut.
• n_jobsest soit un entier, soit None. Il représente le nombre de tâches utilisées dans le calcul parallèle. La valeur par défaut est None, ce qui signifie généralement un travail. -1signifie utiliser tous les processeurs disponibles.

Votre modeltel que défini ci-dessus utilise les valeurs par défaut de tous les paramètres.

Il est temps de commencer à utiliser le modèle. Dans un premier temps, vous devez faire appel .fit()à model:

>>> model.fit(x, y)
LinearRegression()

Avec .fit(), vous calculez les valeurs optimales des poids 𝑏₀ et 𝑏₁, en utilisant l’entrée et la sortie existantes, xet y, comme arguments. En d’autres termes, .fit() cela correspond au modèle . Il renvoie self, qui est la variable modelelle-même. C’est pourquoi vous pouvez remplacer les deux dernières instructions par celle-ci :

>>> model = LinearRegression().fit(x, y)

Cette déclaration fait la même chose que les deux précédentes. C’est juste plus court.

Étape 4 : Obtenez des résultats

Une fois votre modèle ajusté, vous pouvez obtenir les résultats pour vérifier si le modèle fonctionne de manière satisfaisante et l’interpréter.

Vous pouvez obtenir le coefficient de détermination, 𝑅², en .score()faisant appel à model:

>>> r_sq = model.score(x, y)
>>> print(f"coefficient of determination: {r_sq}")
coefficient of determination: 0.7158756137479542

Lorsque vous appliquez .score(), les arguments sont également le prédicteur xet la réponse y, et la valeur de retour est 𝑅².

Les attributs de modelsont .intercept_, qui représente le coefficient 𝑏₀, et .coef_, qui représente 𝑏₁ :

>>> print(f"intercept: {model.intercept_}")
intercept: 5.633333333333329

>>> print(f"slope: {model.coef_}")
slope: [0.54]

Le code ci-dessus illustre comment obtenir 𝑏₀ et 𝑏₁. Vous pouvez remarquer qu’il .intercept_s’agit d’un scalaire, tandis que .coef_c’est un tableau.

La valeur de 𝑏₀ est d’environ 5,63. Cela montre que votre modèle prédit la réponse 5,63 lorsque 𝑥 est zéro. La valeur 𝑏₁ = 0,54 signifie que la réponse prédite augmente de 0,54 lorsque 𝑥 est augmenté de un.

Vous remarquerez que vous pouvez yégalement fournir un tableau bidimensionnel. Dans ce cas, vous obtiendrez un résultat similaire. Voici à quoi cela pourrait ressembler :

>>> new_model = LinearRegression().fit(x, y.reshape((-1, 1)))
>>> print(f"intercept: {new_model.intercept_}")
intercept: [5.63333333]

>>> print(f"slope: {new_model.coef_}")
slope: [[0.54]]

Comme vous pouvez le voir, cet exemple est très similaire au précédent, mais dans ce cas, .intercept_il s’agit d’un tableau unidimensionnel avec l’élément unique 𝑏₀, et .coef_d’un tableau bidimensionnel avec l’élément unique 𝑏₁.

Étape 5 : Prédire la réponse

Une fois que vous disposez d’un modèle satisfaisant, vous pouvez l’utiliser pour des prédictions avec des données existantes ou nouvelles. Pour obtenir la réponse prédite, utilisez.predict() :

>>> y_pred = model.predict(x)
>>> print(f"predicted response:\n{y_pred}")
predicted response:
[ 8.33333333 13.73333333 19.13333333 24.53333333 29.93333333 35.33333333]

Lors de l’application .predict(), vous transmettez le régresseur comme argument et obtenez la réponse prédite correspondante. Il s’agit d’une manière presque identique de prédire la réponse :

>>> y_pred = model.intercept_ + model.coef_ * x
>>> print(f"predicted response:\n{y_pred}")
predicted response:
[[ 8.33333333]
 [13.73333333]
 [19.13333333]
 [24.53333333]
 [29.93333333]
 [35.33333333]]

Dans ce cas, vous multipliez chaque élément de xavec model.coef_et ajoutez model.intercept_au produit.

Le résultat ici diffère de l’exemple précédent uniquement par les dimensions. La réponse prédite est désormais un tableau à deux dimensions, alors que dans le cas précédent, elle avait une seule dimension.

Si vous réduisez le nombre de dimensions xà une, alors ces deux approches donneront le même résultat. Vous pouvez le faire en le remplaçant xpar x.reshape(-1), x.flatten()ou x.ravel()en le multipliant par model.coef_.

En pratique, les modèles de régression sont souvent appliqués aux prévisions. Cela signifie que vous pouvez utiliser des modèles ajustés pour calculer les sorties en fonction de nouvelles entrées :

>>> x_new = np.arange(5).reshape((-1, 1))
>>> x_new
array([[0],
       [1],
       [2],
       [3],
       [4]])

>>> y_new = model.predict(x_new)
>>> y_new
array([5.63333333, 6.17333333, 6.71333333, 7.25333333, 7.79333333])

Ici .predict()est appliqué au nouveau régresseur x_newet donne la réponse y_new. Cet exemple utilise commodément arange()from numpypour générer un tableau avec les éléments de 0, inclus, jusqu’à 5 excluant, c’est-à-dire , 0, 1, 2, 3et 4.

Vous pouvez trouver plus d’informations LinearRegressionsur la page de documentation officielle .

Régression linéaire multiple avec scikit-learn

Vous pouvez implémenter une régression linéaire multiple en suivant les mêmes étapes que pour une régression simple. La principale différence est que votre xtableau comportera désormais deux colonnes ou plus.

Étapes 1 et 2 : importer des packages et des classes et fournir des données

Tout d’abord, vous importez numpyet sklearn.linear_model.LinearRegressionfournissez des entrées et des sorties connues :

>>> import numpy as np
>>> from sklearn.linear_model import LinearRegression

>>> x = [
...   [0, 1], [5, 1], [15, 2], [25, 5], [35, 11], [45, 15], [55, 34], [60, 35]
... ]
>>> y = [4, 5, 20, 14, 32, 22, 38, 43]
>>> x, y = np.array(x), np.array(y)

C’est une façon simple de définir l’entrée xet la sortie y. Vous pouvez imprimer xet yvoir à quoi ils ressemblent maintenant :

>>> x
array([[ 0,  1],
       [ 5,  1],
       [15,  2],
       [25,  5],
       [35, 11],
       [45, 15],
       [55, 34],
       [60, 35]])

>>> y
array([ 4,  5, 20, 14, 32, 22, 38, 43])

Dans la régression linéaire multiple, xil s’agit d’un tableau à deux dimensions avec au moins deux colonnes, alors yqu’il s’agit généralement d’un tableau à une dimension. Il s’agit d’un exemple simple de régression linéaire multiple et xcomporte exactement deux colonnes.

Étape 3 : Créez un modèle et ajustez-le

L’étape suivante consiste à créer le modèle de régression en tant qu’instance de LinearRegressionet à l’adapter à.fit() :

>>> model = LinearRegression().fit(x, y)

Le résultat de cette instruction est la variable modelfaisant référence à l’objet de type LinearRegression. Il représente le modèle de régression ajusté avec les données existantes.

Étape 4 : Obtenez des résultats

Vous pouvez obtenir les propriétés du modèle de la même manière que dans le cas d’une régression linéaire simple :

>>> r_sq = model.score(x, y)
>>> print(f"coefficient of determination: {r_sq}")
coefficient of determination: 0.8615939258756776

>>> print(f"intercept: {model.intercept_}")
intercept: 5.52257927519819

>>> print(f"coefficients: {model.coef_}")
coefficients: [0.44706965 0.25502548]

Vous obtenez la valeur de 𝑅² en utilisant .score()et les valeurs des estimateurs des coefficients de régression avec .intercept_et .coef_. Encore une fois, .intercept_le biais est valable 𝑏₀, alors que maintenant .coef_c’est un tableau contenant 𝑏₁ et 𝑏₂.

Dans cet exemple, l’ordonnée à l’origine est d’environ 5,52, et c’est la valeur de la réponse prédite lorsque 𝑥₁ = 𝑥₂ = 0. Une augmentation de 𝑥₁ de 1 donne une augmentation de la réponse prédite de 0,45. De même, lorsque 𝑥₂ augmente de 1, la réponse augmente de 0,26.

Étape 5 : Prédire la réponse

Les prédictions fonctionnent également de la même manière que dans le cas d’une régression linéaire simple :

>>> y_pred = model.predict(x)
>>> print(f"predicted response:\n{y_pred}")
predicted response:
[ 5.77760476  8.012953   12.73867497 17.9744479  23.97529728 29.4660957
 38.78227633 41.27265006]

La réponse prédite est obtenue avec .predict(), ce qui équivaut à ce qui suit :

>>> y_pred = model.intercept_ + np.sum(model.coef_ * x, axis=1)
>>> print(f"predicted response:\n{y_pred}")
predicted response:
[ 5.77760476  8.012953   12.73867497 17.9744479  23.97529728 29.4660957
 38.78227633 41.27265006]

Vous pouvez prédire les valeurs de sortie en multipliant chaque colonne de l’entrée avec le poids approprié, en additionnant les résultats et en ajoutant l’ordonnée à l’origine à la somme.

Vous pouvez également appliquer ce modèle à de nouvelles données :

>>> x_new = np.arange(10).reshape((-1, 2))
>>> x_new
array([[0, 1],
       [2, 3],
       [4, 5],
       [6, 7],
       [8, 9]])

>>> y_new = model.predict(x_new)
>>> y_new
array([ 5.77760476,  7.18179502,  8.58598528,  9.99017554, 11.3943658 ])

C’est la prédiction utilisant un modèle de régression linéaire.

Régression polynomiale avec scikit-learn

La mise en œuvre d’une régression polynomiale avec scikit-learn est très similaire à la régression linéaire. Il n’y a qu’une seule étape supplémentaire : vous devez transformer le tableau d’entrées pour inclure des termes non linéaires tels que 𝑥².

Étape 1 : Importer des packages et des classes

En plus de numpyet sklearn.linear_model.LinearRegression, vous devez également importer la classe PolynomialFeaturesdepuissklearn.preprocessing :

>>> import numpy as np
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.preprocessing import PolynomialFeatures

L’importation est maintenant terminée et vous disposez de tout ce dont vous avez besoin pour travailler.

Étape 2a : Fournissez les données

Cette étape définit l’entrée et la sortie et est la même que dans le cas d’une régression linéaire :

>>> x = np.array([5, 15, 25, 35, 45, 55]).reshape((-1, 1))
>>> y = np.array([15, 11, 2, 8, 25, 32])

Vous disposez désormais de l’entrée et de la sortie dans un format approprié. Gardez à l’esprit que l’entrée doit être un tableau à deux dimensions . C’est pourquoi .reshape()est utilisé.

Étape 2b : Transformer les données d’entrée

C’est la nouvelle étape que vous devez implémenter pour la régression polynomiale !

Comme vous l’avez appris plus tôt, vous devez inclure 𝑥² – et peut-être d’autres termes – comme fonctionnalités supplémentaires lors de la mise en œuvre de la régression polynomiale. Pour cette raison, vous devez transformer le tableau d’entrée xpour contenir des colonnes supplémentaires avec les valeurs de 𝑥², et éventuellement plus d’entités.

Il est possible de transformer le tableau d’entrée de plusieurs manières, par exemple en utilisant insert()from numpy. Mais le cours PolynomialFeaturesest très pratique à cet effet. Allez-y et créez une instance de cette classe :

>>> transformer = PolynomialFeatures(degree=2, include_bias=False)

La variable transformerfait référence à une instance de PolynomialFeaturescelle que vous pouvez utiliser pour transformer l’entrée x.

Vous pouvez fournir plusieurs paramètres facultatifs pourPolynomialFeatures :

• degreeest un entier ( 2par défaut) qui représente le degré de la fonction de régression polynomiale.
• interaction_onlyest un booléen ( Falsepar défaut) qui décide d’inclure uniquement les fonctionnalités d’interaction ( True) ou toutes les fonctionnalités ( False).
• include_biasest un booléen ( Truepar défaut) qui décide d’inclure ou non la colonne de 1valeurs de biais ou d’interception ( ).TrueFalse

Cet exemple utilise les valeurs par défaut de tous les paramètres sauf include_bias. Vous souhaiterez parfois expérimenter le degré de la fonction, et il peut quand même être bénéfique pour la lisibilité de fournir cet argument.

Avant de postuler transformer, vous devez l’équiper de .fit():

>>> transformer.fit(x)
PolynomialFeatures(include_bias=False)

Une fois transformerinstallé, il est prêt à créer un nouveau tableau d’entrée modifié. Vous postulez .transform()pour cela :

>>> x_ = transformer.transform(x)

C’est la transformation du tableau d’entrée avec .transform(). Il prend le tableau d’entrée comme argument et renvoie le tableau modifié.

Vous pouvez également utiliser .fit_transform()pour remplacer les trois instructions précédentes par une seule :

>>> x_ = PolynomialFeatures(degree=2, include_bias=False).fit_transform(x)

Avec .fit_transform(), vous ajustez et transformez le tableau d’entrée en une seule instruction. Cette méthode prend également le tableau d’entrée et fait effectivement la même chose que .fit()celle .transform()appelée dans cet ordre. Il renvoie également le tableau modifié. Voici à quoi ressemble le nouveau tableau d’entrée :

>>> x_
array([[   5.,   25.],
       [  15.,  225.],
       [  25.,  625.],
       [  35., 1225.],
       [  45., 2025.],
       [  55., 3025.]])

Le tableau d’entrée modifié contient deux colonnes : une avec les entrées d’origine et l’autre avec leurs carrés. Vous pouvez trouver plus d’informations PolynomialFeaturessur la page de documentation officielle .

Étape 3 : Créez un modèle et ajustez-le

Cette étape est également la même que dans le cas d’une régression linéaire. Vous créez et ajustez le modèle :

>>> model = LinearRegression().fit(x_, y)

Le modèle de régression est maintenant créé et ajusté. Il est prêt à être appliqué. Vous devez garder à l’esprit que le premier argument de .fit()est le tableau d’entrée modifié x_ et non l’original x.

Étape 4 : Obtenez des résultats

Vous pouvez obtenir les propriétés du modèle de la même manière que dans le cas d’une régression linéaire :

>>> r_sq = model.score(x_, y)
>>> print(f"coefficient of determination: {r_sq}")
coefficient of determination: 0.8908516262498563

>>> print(f"intercept: {model.intercept_}")
intercept: 21.372321428571436

>>> print(f"coefficients: {model.coef_}")
coefficients: [-1.32357143  0.02839286]

Encore une fois, .score()cela renvoie 𝑅². Son premier argument est également l’entrée modifiée x_, pas x. Les valeurs des poids sont associées à .intercept_et .coef_. Ici, .intercept_représente 𝑏₀, tandis que .coef_fait référence au tableau qui contient 𝑏₁ et 𝑏₂.

Vous pouvez obtenir un résultat très similaire avec différents arguments de transformation et de régression :

>>> x_ = PolynomialFeatures(degree=2, include_bias=True).fit_transform(x)

Si vous appelez PolynomialFeaturesavec le paramètre par défaut include_bias=True, ou si vous l’omettez simplement, vous obtiendrez le nouveau tableau d’entrée x_avec la colonne supplémentaire la plus à gauche contenant uniquement 1des valeurs. Cette colonne correspond à l’interception. Voici à quoi ressemble le tableau d’entrée modifié dans ce cas :

>>> x_
array([[1.000e+00, 5.000e+00, 2.500e+01],
       [1.000e+00, 1.500e+01, 2.250e+02],
       [1.000e+00, 2.500e+01, 6.250e+02],
       [1.000e+00, 3.500e+01, 1.225e+03],
       [1.000e+00, 4.500e+01, 2.025e+03],
       [1.000e+00, 5.500e+01, 3.025e+03]])

La première colonne x_contient les uns, la seconde contient les valeurs de x, tandis que la troisième contient les carrés de x.

L’interception est déjà incluse dans la colonne la plus à gauche, et vous n’avez pas besoin de l’inclure à nouveau lors de la création de l’instance de LinearRegression. Ainsi, vous pouvez fournir fit_intercept=False. Voici à quoi ressemble la déclaration suivante :

>>> model = LinearRegression(fit_intercept=False).fit(x_, y)

La variable modelcorrespond à nouveau au nouveau tableau d’entrée x_. Par conséquent, x_doit être passé comme premier argument au lieu de x.

Cette approche donne les résultats suivants, qui sont similaires au cas précédent :

>>> r_sq = model.score(x_, y)
>>> print(f"coefficient of determination: {r_sq}")
coefficient of determination: 0.8908516262498564

>>> print(f"intercept: {model.intercept_}")
intercept: 0.0

>>> print(f"coefficients: {model.coef_}")
coefficients: [21.37232143 -1.32357143  0.02839286]

Vous voyez que maintenant .intercept_est nul, mais .coef_contient en fait 𝑏₀ comme premier élément. Tout le reste est identique.

Étape 5 : Prédire la réponse

Si vous souhaitez obtenir la réponse prévue, utilisez simplement .predict(), mais rappelez-vous que l’argument doit être l’entrée modifiée x_au lieu de l’ancienx :

>>> y_pred = model.predict(x_)
>>> print(f"predicted response:\n{y_pred}")
predicted response:
[15.46428571  7.90714286  6.02857143  9.82857143 19.30714286 34.46428571]

Comme vous pouvez le constater, la prédiction fonctionne presque de la même manière que dans le cas d’une régression linéaire. Cela nécessite simplement l’entrée modifiée au lieu de l’original.

Vous pouvez appliquer une procédure identique si vous disposez de plusieurs variables d’entrée . Vous aurez un tableau d’entrée avec plus d’une colonne, mais tout le reste sera pareil. Voici un exemple :

>>> # Step 1: Import packages and classes
>>> import numpy as np
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.preprocessing import PolynomialFeatures

>>> # Step 2a: Provide data
>>> x = [
...   [0, 1], [5, 1], [15, 2], [25, 5], [35, 11], [45, 15], [55, 34], [60, 35]
... ]
>>> y = [4, 5, 20, 14, 32, 22, 38, 43]
>>> x, y = np.array(x), np.array(y)

>>> # Step 2b: Transform input data
>>> x_ = PolynomialFeatures(degree=2, include_bias=False).fit_transform(x)

>>> # Step 3: Create a model and fit it
>>> model = LinearRegression().fit(x_, y)

>>> # Step 4: Get results
>>> r_sq = model.score(x_, y)
>>> intercept, coefficients = model.intercept_, model.coef_

>>> # Step 5: Predict response
>>> y_pred = model.predict(x_)

Cet exemple de régression produit les résultats et prédictions suivants :

>>> print(f"coefficient of determination: {r_sq}")
coefficient of determination: 0.9453701449127822

>>> print(f"intercept: {intercept}")
intercept: 0.8430556452395876

>>> print(f"coefficients:\n{coefficients}")
coefficients:
[ 2.44828275  0.16160353 -0.15259677  0.47928683 -0.4641851 ]

>>> print(f"predicted response:\n{y_pred}")
predicted response:
[ 0.54047408 11.36340283 16.07809622 15.79139    29.73858619 23.50834636
 39.05631386 41.92339046]

Dans ce cas, il existe six coefficients de régression, y compris l’ordonnée à l’origine, comme le montre la fonction de régression estimée 𝑓(𝑥₁, 𝑥₂) = 𝑏₀ + 𝑏₁𝑥₁ + 𝑏₂𝑥₂ + 𝑏₃𝑥₁² + 𝑏₄𝑥₁ 𝑥₂ + 𝑏₅𝑥₂².

Vous pouvez également remarquer que la régression polynomiale a donné un coefficient de détermination plus élevé que la régression linéaire multiple pour le même problème. Au début, on pourrait penser qu’obtenir un si grand 𝑅² est un excellent résultat. Ça pourrait être.

Cependant, dans des situations réelles, avoir un modèle complexe et 𝑅² très proche de un peut également être un signe de surajustement. Pour vérifier les performances d’un modèle, vous devez le tester avec de nouvelles données, c’est-à-dire avec des observations non utilisées pour ajuster ou entraîner le modèle. Pour savoir comment diviser votre ensemble de données en sous-ensembles de formation et de test, consultez Fractionner votre ensemble de données avec train_test_split() de scikit-learn .

Régression linéaire avancée avec des modèles de statistiques

Vous pouvez également implémenter la régression linéaire en Python en utilisant le package statsmodels. Cela est généralement souhaitable lorsque vous avez besoin de résultats plus détaillés.

La procédure est similaire à celle de scikit-learn.

Étape 1 : Importer des packages

Vous devez d’abord effectuer quelques importations. En plus de numpy, vous devez importer statsmodels.api:

>>> import numpy as np
>>> import statsmodels.api as sm

Vous disposez désormais des packages dont vous avez besoin.

Étape 2 : Fournir les données et transformer les entrées

Vous pouvez fournir les entrées et les sorties de la même manière que lorsque vous utilisiez scikit-learn :

>>> x = [
...   [0, 1], [5, 1], [15, 2], [25, 5], [35, 11], [45, 15], [55, 34], [60, 35]
... ]
>>> y = [4, 5, 20, 14, 32, 22, 38, 43]
>>> x, y = np.array(x), np.array(y)

Les tableaux d’entrée et de sortie sont créés, mais le travail n’est pas encore terminé.

Vous devez ajouter la colonne des uns aux entrées si vous souhaitez que les modèles statistiques calculent l’ordonnée à l’origine 𝑏₀. Il ne prend pas en compte 𝑏₀ par défaut. Ceci est juste un appel de fonction :

>>> x = sm.add_constant(x)

C’est ainsi que vous ajoutez la colonne des uns xavec add_constant(). Il prend le tableau d’entrée xcomme argument et renvoie un nouveau tableau avec la colonne de ceux insérés au début. Voici comment xet yregardez maintenant :

>>> x
array([[ 1.,  0.,  1.],
       [ 1.,  5.,  1.],
       [ 1., 15.,  2.],
       [ 1., 25.,  5.],
       [ 1., 35., 11.],
       [ 1., 45., 15.],
       [ 1., 55., 34.],
       [ 1., 60., 35.]])

>>> y
array([ 4,  5, 20, 14, 32, 22, 38, 43])

Vous pouvez voir que la version modifiée xcomporte trois colonnes : la première colonne de uns, correspondant à 𝑏₀ et remplaçant l’ordonnée à l’origine, ainsi que deux colonnes des caractéristiques d’origine.

Étape 3 : Créez un modèle et ajustez-le

Le modèle de régression basé sur les moindres carrés ordinaires est une instance de la classe statsmodels.regression.linear_model.OLS. Voici comment vous en procurer un :

>>> model = sm.OLS(y, x)

Il faut être prudent ici ! Notez que le premier argument est la sortie, suivi de l’entrée. C’est l’ordre inverse des fonctions scikit-learn correspondantes.

Il existe plusieurs autres paramètres facultatifs. Pour trouver plus d’informations sur cette classe, vous pouvez visiter la page de documentation officielle .

Une fois votre modèle créé, vous pouvez alors appliquer .fit()dessus :

>>> results = model.fit()

En appelant .fit(), vous obtenez la variable results, qui est une instance de la classe statsmodels.regression.linear_model.RegressionResultsWrapper. Cet objet contient de nombreuses informations sur le modèle de régression.

Étape 4 : Obtenez des résultats

La variable resultsfait référence à l’objet qui contient des informations détaillées sur les résultats de la régression linéaire. Expliquer ces résultats dépasse largement le cadre de ce didacticiel, mais vous apprendrez ici comment les extraire.

Vous pouvez appeler .summary()pour obtenir le tableau avec les résultats de la régression linéaire :

>>> print(results.summary())
OLS Regression Results
=============================================================================
Dep. Variable:                     y   R-squared:                       0.862
Model:                           OLS   Adj. R-squared:                  0.806
Method:                Least Squares   F-statistic:                     15.56
Date:               Thu, 12 May 2022   Prob (F-statistic):            0.00713
Time:                       14:15:07   Log-Likelihood:                -24.316
No. Observations:                  8   AIC:                             54.63
Df Residuals:                      5   BIC:                             54.87
Df Model:                          2
Covariance Type:           nonrobust
=============================================================================
                coef    std err          t      P>|t|      [0.025      0.975]
-----------------------------------------------------------------------------
const         5.5226      4.431      1.246      0.268      -5.867      16.912
x1            0.4471      0.285      1.567      0.178      -0.286       1.180
x2            0.2550      0.453      0.563      0.598      -0.910       1.420
=============================================================================
Omnibus:                       0.561   Durbin-Watson:                   3.268
Prob(Omnibus):                 0.755   Jarque-Bera (JB):                0.534
Skew:                          0.380   Prob(JB):                        0.766
Kurtosis:                      1.987   Cond. No.                         80.1
=============================================================================

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is
    correctly specified.

Ce tableau est très complet. Vous pouvez trouver de nombreuses valeurs statistiques associées à la régression linéaire, notamment 𝑅², 𝑏₀, 𝑏₁ et 𝑏₂.

Dans ce cas particulier, vous pourriez recevoir un avertissement indiquant kurtosistest only valid for n>=20. Cela est dû au petit nombre d’observations fournies dans l’exemple.

Vous pouvez extraire n’importe laquelle des valeurs du tableau ci-dessus. Voici un exemple :

>>> print(f"coefficient of determination: {results.rsquared}")
coefficient of determination: 0.8615939258756776

>>> print(f"adjusted coefficient of determination: {results.rsquared_adj}")
adjusted coefficient of determination: 0.8062314962259487

>>> print(f"regression coefficients: {results.params}")
regression coefficients: [5.52257928 0.44706965 0.25502548]

C’est ainsi que vous obtenez certains des résultats de la régression linéaire :

1. .rsquaredcontient 𝑅².
2. .rsquared_adjreprésente 𝑅² ajusté, c’est-à-dire 𝑅² corrigé en fonction du nombre d’entités en entrée.
3. .paramsfait référence au tableau avec 𝑏₀, 𝑏₁ et 𝑏₂.

Vous pouvez également remarquer que ces résultats sont identiques à ceux obtenus avec scikit-learn pour le même problème.

Pour trouver plus d’informations sur les résultats de la régression linéaire, veuillez visiter la page de documentation officielle .

Étape 5 : Prédire la réponse

Vous pouvez obtenir la réponse prévue sur les valeurs d’entrée utilisées pour créer le modèle en utilisant .fittedvaluesou .predict()avec le tableau d’entrée comme argument :

>>> print(f"predicted response:\n{results.fittedvalues}")
predicted response:
[ 5.77760476  8.012953   12.73867497 17.9744479  23.97529728 29.4660957
 38.78227633 41.27265006]

>>> print(f"predicted response:\n{results.predict(x)}")
predicted response:
[ 5.77760476  8.012953   12.73867497 17.9744479  23.97529728 29.4660957
 38.78227633 41.27265006]

Il s’agit de la réponse prévue pour les entrées connues. Si vous souhaitez des prédictions avec de nouveaux régresseurs, vous pouvez également appliquer .predict()de nouvelles données comme argument :

>>> x_new = sm.add_constant(np.arange(10).reshape((-1, 2)))
>>> x_new
array([[1., 0., 1.],
       [1., 2., 3.],
       [1., 4., 5.],
       [1., 6., 7.],
       [1., 8., 9.]])

>>> y_new = results.predict(x_new)
>>> y_new
array([ 5.77760476,  7.18179502,  8.58598528,  9.99017554, 11.3943658 ])

Vous pouvez remarquer que les résultats prédits sont les mêmes que ceux obtenus avec scikit-learn pour le même problème.

Au-delà de la régression linéaire

La régression linéaire n’est parfois pas appropriée, notamment pour les modèles non linéaires de grande complexité.

Heureusement, il existe d’autres techniques de régression adaptées aux cas où la régression linéaire ne fonctionne pas bien. Certains d’entre eux sont des machines vectorielles de support, des arbres de décision, des forêts aléatoires et des réseaux de neurones.

Il existe de nombreuses bibliothèques Python pour la régression utilisant ces techniques. La plupart d’entre eux sont gratuits et open source. C’est l’une des raisons pour lesquelles Python fait partie des principaux langages de programmation pour l’apprentissage automatique.

Le package scikit-learn fournit les moyens d’utiliser d’autres techniques de régression d’une manière très similaire à ce que vous avez vu. Il contient des classes pour les machines à vecteurs de support , les arbres de décision , les forêts aléatoires , etc., avec les méthodes .fit(), .predict(), .score(), etc.

Conclusion

Vous savez maintenant ce qu’est la régression linéaire et comment l’implémenter avec Python et trois packages open source : NumPy, scikit-learn et statsmodels. Vous utilisez NumPy pour gérer les tableaux. La régression linéaire est implémentée avec les éléments suivants :

• scikit-learn si vous n’avez pas besoin de résultats détaillés et souhaitez utiliser l’approche cohérente avec d’autres techniques de régression
• statsmodels si vous avez besoin des paramètres statistiques avancés d’un modèle

Les deux approches méritent d’être apprises à utiliser et à explorer davantage. Les liens dans cet article peuvent être très utiles pour cela.

Dans ce didacticiel, vous avez appris les étapes suivantes pour effectuer une régression linéaire en Python :

1. Importez les packages et les classes dont vous avez besoin
2. Fournir des données avec lesquelles travailler et éventuellement effectuer les transformations appropriées
3. Créez un modèle de régression et adaptez-le aux données existantes
4. Vérifiez les résultats de l’ajustement du modèle pour savoir si le modèle est satisfaisant
5. Appliquer le modèle pour les prédictions

Et avec ça, vous êtes prêt à partir ! Si vous avez des questions ou des commentaires, veuillez les mettre dans la section commentaires ci-dessous.

A propos de l’auteur